I didn’t find math particularly exciting when I was in high school. To be honest, I only studied it when I went to university because it initially seemed quite easy to me. But in my very first math lecture as an undergraduate, I realized that everything I thought I knew about math was wrong. It was anything but easy. Mathematics, I soon discovered, can be really exciting—especially if you go beyond the realm of pure arithmetic.
In physics, the truly surprising content—concepts that go against your intuition about the universe—emerges around high school, when students can glimpse the strange quantum world and encounter Einstein’s general and special theories of relativity. School mathematics cannot keep up with these wonders. You learn elementary arithmetic operations, integration and derivation, the basic handling of probabilities and vectors. If you’re lucky, ambitious teachers might show you a simple proof. And that’s it. So it’s no wonder that many pupils fail to develop a real passion for the subject.
Yet mathematics offers all sorts of surprises, such as the Banach-Tarski paradox, which states that you can double a sphere almost magically, or the fact that there are infinitely many different infinities. What really blew me away was discovering how deeply mathematics is interwoven with the strangest physical phenomena. It’s not necessarily quantum physics itself that gives rise to the incredible effects; no, the systems always follow the strict rules of mathematics. As chemist Peter Atkins put it in his 2003 book Galileo’s Finger, “Determining where mathematics ends and science begins is as difficult, and as pointless, as mapping the edge of a morning mist.”
On supporting science journalism
If you’re enjoying this article, consider supporting our award-winning journalism by subscribing. By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.
Few examples illustrate the mixing of math and physics better than a discovery made by physicist Michael Berry. In 1984 Berry revealed a profound and largely unexpected geometric side to quantum mechanics. This geometry, Berry realized, gives quantum particles a kind of memory.
Nothing Should Actually Happen
At the time, Berry was investigating a very simple system: the quantum state of a particle, such as a neutron, in a changing environment. Neutrons have a quantum property called spin, which acts like a tiny magnet that the particles carry with them. This spin can either be oriented with the north pole facing upward or downward—so physicists speak of neutrons having “spin up” or “spin down.” The spin of a neutron is influenced by external magnetic fields.
Berry used mathematical means to investigate what would happen to the neutron if the direction of the magnetic field changed slowly. According to the so-called adiabatic theorem, which was introduced in the early 20th century, the quantum properties of the particle should not change as a result: its energy, momentum, mass and spin remain the same.
If you slowly turn the direction of the magnetic field and then move it back in the original direction, this action should, in principle, not actually change anything. “That, at any rate, was the prevalent opinion among physicists for many years,” wrote Berry in an article in Scientific American in December 1988. But a “change on the phase of a wave function was overlooked.”
One of the strangest phenomena of quantum mechanics is wave-particle duality: quantum objects can be imagined as pointlike shapes, but they also exhibit wave behavior like water. A phase describes a displacement of the wave by a certain angle—for example, the cosine function is nothing other than a phase-shifted sine function.
As Berry recognized in his calculations, a slow change in the magnetic field causes the wave function of the neutron to rotate by a certain phase. This means that the wave function of the particle shows what happened in the past (in this case, the change in the magnetic field). Further, Berry recognized that this phase does not only occur in the special case of a particle in a magnetic field. Various situations in which a quantum system is slowly changed and then returned to its original conditions leave traces in the wave function.
Experiments conducted shortly after Berry’s groundbreaking work was published confirmed these ideas. If you are familiar with quantum mechanics, then you probably know that the wave function is not a directly observable quantity. Nevertheless, there is a way to measure the phase shift by using a second particle as a reference. In these experiments, physicists allowed for the collision of two particles, such as neutrons, one of which had previously been in a variable magnetic field. When the neutrons met, their wave functions interacted.
These functions behave like water waves: if the troughs and peaks align, they strengthen each other; if, on the other hand, they are shifted against each other, they can weaken or die out completely. These phenomena are known as constructive or destructive interference, respectively.
The experiments revealed that Berry was correct: the neutrons were out of phase, interfering destructively. That observation indicated that one of the particles had briefly been in a changing magnetic field. Even though none of its measurable properties had changed directly as a result, its altered wave function gave it away.
The Curved Universe
But how did Berry know that the particles would undergo a phase shift? In fact, such a phase appears wherever there is curvature. That’s why phase plays an important role in Einstein’s general theory of relativity—the theory he used to describe gravity.
Some experts contend that general relativity is more geometry than physics. According to this theory, matter bends spacetime, and this deformation causes masses to attract each other—a phenomenon that we perceive as gravity. I like to think of it as a rubber sheet on which heavy objects are placed, deforming the sheet and thus influencing the objects. This visualization has some weaknesses, however: spacetime is two-dimensional in this conception, and I look down on it from my three-dimensional world. General relativity, on the other hand, describes the curvature of four-dimensional spacetime without looking at it from a five-dimensional perspective.
This raises the question of how you can deduce the curvature of something if you cannot look at the object from the outside. The phase that Berry observed helps here.
Suppose I wanted to prove in a complicated way that Earth is a sphere. To do this, I can walk straight north from my location somewhere in Germany over mountains, valleys, rivers, lakes and oceans. In this thought experiment, nothing can keep me from following a straight path. When I reach the North Pole, I move right without turning around by walking sideways like a crab. I walk until I end up at the same latitude from which I started. I then follow the latitude to the left—again without turning—until I arrive back at the starting point. Although I land at my original place, I no longer face north, as I did at the beginning, but east. So this round trip hasn’t changed me as a person (except perhaps for the physical exertion), yet I have turned by a certain angle.
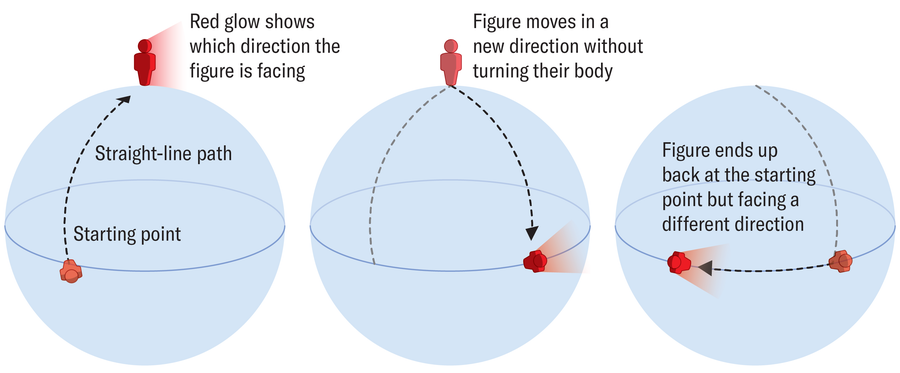
If I had followed the same path on a flat plane, I would have returned to the starting point without any rotation. But in this thought experiment, set on our curved planet, the same thing happens to me as to the wave function in Berry’s theory: it receives a phase, an angle that shifts it.
The angle that I picked up during my travels depends solely on the geometry of Earth. Its value is proportional to the area enclosed by my path. Because nothing else influences the phase—neither my speed nor whether I take a break—it is referred to as the “geometric phase.”
For mathematicians, this was nothing new at the time Berry published his work. They had known about the concept for many decades. But nobody had applied geometric phases to quantum-mechanical processes. The phase in the wave function reveals the geometry of the so-called parameter space. This is an abstract, high-dimensional space that combines all parameters that can influence the wave function (such as magnetic field, energy, location and speed). The short-term change in the direction of a magnetic field (or another parameter) describes a closed curve in this space—just like my circular path on the globe. Because this parameter space is usually curved, this leaves traces in the wave function.
“The geometric phase can therefore be regarded as the best answer the system can offer to the question ‘What path in parameter space did the system take?” Berry wrote in his 1988 Scientific American article. “In this sense it is a kind of quantum ‘memory.’”
Berry had thus revealed a profound connection between quantum systems and geometry, which turned out to be extremely valuable. The Berry phase, named after him, can be used to explain phenomena such as the quantum Hall effect, which occurs in certain solids and raised many questions before Berry’s discovery.
All of this is extremely exciting. For me, however, the most impressive thing is that Berry established the new research field of geometric quantum physics by drawing on existing mathematical concepts. He didn’t have to add anything new to physics or mathematics—instead mathematics made it possible to reveal something completely unexpected in physics.
This article originally appeared in Spektrum der Wissenschaft and was reproduced with permission.
